This article is an application of the article “Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering by Belkin and Niyogi.”
Graphs can be represented via their adjacency matrix and from there on one can use the well-developed field of algebraic graph theory. We show in simple steps how this representation can be used to perform node attribute inference on the Cora citation network.
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
import os
import networkx as nx
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegressionCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score
%matplotlib inline
Dataset
The Cora dataset is the hello-world dataset when looking at graph learning. We have described in details in this article and will not repeat it here. You can also find in the article a direct link to download the data.
The construction below recreates the steps outlined in the article.
data_dir = os.path.expanduser("~/data/cora")
cora_location = os.path.expanduser(os.path.join(data_dir, "cora.cites"))
g_nx = nx.read_edgelist(path=cora_location)
cora_data_location = os.path.expanduser(os.path.join(data_dir, "cora.content"))
node_attr = pd.read_csv(cora_data_location, sep='\t', header=None)
values = { str(row.tolist()[0]): row.tolist()[-1] for _, row in node_attr.iterrows()}
nx.set_node_attributes(g_nx, values, 'subject')
feature_names = ["w_{}".format(ii) for ii in range(1433)]
column_names = feature_names + ["subject"]
node_data = pd.read_table(os.path.join(data_dir, "cora.content"), header=None, names=column_names)
g_nx_ccs = (g_nx.subgraph(c).copy() for c in nx.connected_components(g_nx))
g_nx = max(g_nx_ccs, key=len)
node_ids = list(g_nx.nodes())
print("Largest subgraph statistics: {} nodes, {} edges".format(
g_nx.number_of_nodes(), g_nx.number_of_edges()))
node_targets = [ g_nx.node[node_id]['subject'] for node_id in node_ids]
print(f"There are {len(np.unique(node_targets))} unique labels on the nodes.")
print(f"There are {len(g_nx.nodes())} nodes in the network.")
Largest subgraph statistics: 2485 nodes, 5069 edges
There are 7 unique labels on the nodes.
There are 2485 nodes in the network.
We map the subject to a color for rendering purposes.
colors = {'Case_Based': 'black',
'Genetic_Algorithms': 'red',
'Neural_Networks': 'blue',
'Probabilistic_Methods': 'green',
'Reinforcement_Learning': 'aqua',
'Rule_Learning': 'purple',
'Theory': 'yellow'}
The graph Laplacian
There are at leat 3 graph Laplacians in use. These are called unormalized, random walk and normalised graph Laplacian and they are defined as follows:
- Unormalized: $L = D-A$
- Random Walk: $L_{rw} = D^{-1}L = I – D^{-1}A$
- Normalised: $L_{sym} = D^{-1/2}LD^{-1/2} = I – D^{-1/2}AD^{-1/2}$
We’ll use the unormalised graph Laplacian from here on.
The adjacency matrix of the graph in numpy format:
A = nx.to_numpy_array(g_nx)
and the degree matrix from this:
D = np.diag(A.sum(axis=1))
print(D)
[[168. 0. 0. ... 0. 0. 0.]
[ 0. 5. 0. ... 0. 0. 0.]
[ 0. 0. 6. ... 0. 0. 0.]
...
[ 0. 0. 0. ... 4. 0. 0.]
[ 0. 0. 0. ... 0. 4. 0.]
[ 0. 0. 0. ... 0. 0. 2.]]
So, the unnormalized Laplacian is
L = D-A
print(L)
[[168. -1. -1. ... 0. 0. 0.]
[ -1. 5. 0. ... 0. 0. 0.]
[ -1. 0. 6. ... 0. 0. 0.]
...
[ 0. 0. 0. ... 4. -1. -1.]
[ 0. 0. 0. ... -1. 4. 0.]
[ 0. 0. 0. ... -1. 0. 2.]]
Eigenvectors and eigenvalues of the Laplacian
Numpy can directly give you all you need in one line:
eigenvalues, eigenvectors = np.linalg.eig(L)
In general, eigenvalues can be complex. Only special types of matrices give rise to real values only. So, we’ll take the real parts only and assume that the dropped complex dimension does not contain significant information.
eigenvalues = np.real(eigenvalues)
eigenvectors = np.real(eigenvectors)
Let’s also order the eigenvalues from small to large:
order = np.argsort(eigenvalues)
eigenvalues = eigenvalues[order]
For example, the first eigenvalues are:
eigenvalues[0:10]
array([3.33303173e-15, 1.48014820e-02, 2.36128446e-02, 3.03008575e-02,
4.06458495e-02, 4.72354991e-02, 5.65503673e-02, 6.00350936e-02,
7.24399539e-02, 7.45956530e-02])
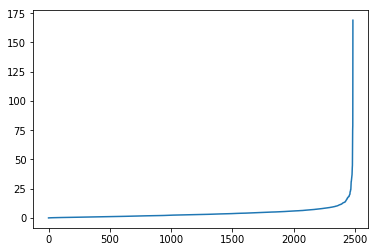
The first eigenvalue is as good as zero and this is a general fact; the smallest eigenvalue is always zero. The reason it’s not exactly zero above is because of computational accuracy.
So, we will omit the first eigenvector since it does not convey any information.
We also take a 32-dimensional subspace of the full vector space:
embedding_size = 32
v_0 = eigenvectors[:, order[0]]
v = eigenvectors[:, order[1:(embedding_size+1)]]
A plot of the eigenvalue looks like the following:
plt.plot(eigenvalues)
Let’s use t-SNE to visualize out 32-dimensional organization:
tsne = TSNE()
v_pr = tsne.fit_transform(v)
alpha=0.7
label_map = { l: i for i, l in enumerate(np.unique(node_targets))}
node_colours = [ label_map[target] for target in node_targets]
fig = plt.figure(figsize=(10,8))
plt.scatter(v_pr[:,0],
v_pr[:,1],
c=node_colours, cmap="jet", alpha=alpha)
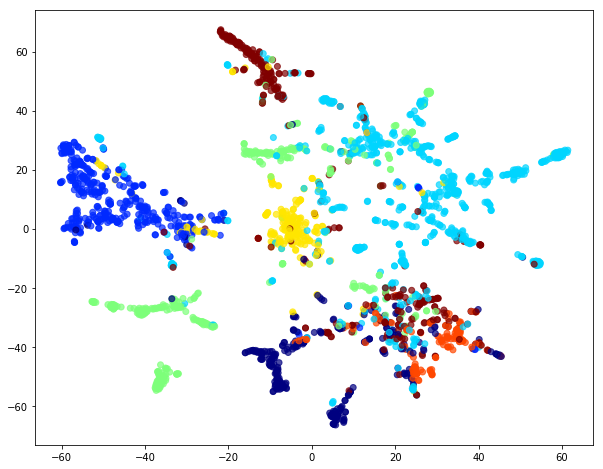
We see that the eigenvectors of the Laplacian form clusters corresponding to the target labels. It means that in principle we can train a model using the eigenvectors and make predictions about an unseen graphs. Simply said, given an unlabelled graph we can extract its Laplacian, feed it to the model and get labels for the nodes.
Training a classifier
The eigenvectors are from the point of view of machine learning just ordinary feature vectors. Taking a training and test set really means in this case taking a subset of the nodes (a subgraph) even though on a code level it’s just an ordinary classifier.
X = v
Y = np.array(node_targets)
clf = RandomForestClassifier(n_estimators=10, min_samples_leaf=4)
X_train, X_test, y_train, y_test = train_test_split(X, Y, train_size=140, random_state=42)
clf.fit(X_train, y_train)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=4, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=None,
oob_score=False, random_state=None, verbose=0,
warm_start=False)
print("score on X_train {}".format(clf.score(X_train, y_train)))
print("score on X_test {}".format(clf.score(X_test, y_test)))
score on X_train 0.8571428571428571
score on X_test 0.7292110874200426
From here on you can experiment with different embedding dimensions, different Laplacians or any other matrix representing the structure of the graph.

