Graph Link Prediction using GraphSAGE
This article is based on the paper “Inductive Representation Learning on Large Graphs” by Hamilton, Ying and Leskovec.
The StellarGraph implementation of the GraphSAGE algorithm is used to build a model that predicts citation links of the Cora dataset.
The way link prediction is turned into a supervised learning task is actually very savvy. Pairs of nodes are embedded and a binary prediction model is trained where ‘1’ means the nodes are connected and ‘0’ means they are not connected. It’s like embedding the adjacency matrix and finding a decision boundary between two types of elements. The entire model is trained end-to-end by minimizing the loss function of choice (e.g., binary cross-entropy between predicted link probabilities and true link labels, with true/false citation links having labels 1/0) using stochastic gradient descent (SGD) updates of the model parameters, with minibatches of ‘training’ links fed into the model.
import networkx as nx
import pandas as pd
import os
import stellargraph as sg
from stellargraph.data import EdgeSplitter
from stellargraph.mapper import GraphSAGELinkGenerator
from stellargraph.layer import GraphSAGE, link_classification
import tensorflow.keras as keras # DO NOT USE KERAS DIRECTLY
from sklearn import preprocessing, feature_extraction, model_selection
from stellargraph import globalvar
Dataset
The Cora dataset is the hello-world dataset when looking at graph learning. We have described in details in this article and will not repeat it here. You can also find in the article a direct link to download the data.
The construction below recreates the steps outlined in the article.
data_dir = os.path.expanduser("~/data/cora")
cora_location = os.path.expanduser(os.path.join(data_dir, "cora.cites"))
g_nx = nx.read_edgelist(path=cora_location)
cora_data_location = os.path.expanduser(os.path.join(data_dir, "cora.content"))
node_attr = pd.read_csv(cora_data_location, sep='\t', header=None)
values = { str(row.tolist()[0]): row.tolist()[-1] for _, row in node_attr.iterrows()}
nx.set_node_attributes(g_nx, values, 'subject')
g_nx_ccs = (g_nx.subgraph(c).copy() for c in nx.connected_components(g_nx))
g_nx = max(g_nx_ccs, key=len)
print("Largest connected component: {} nodes, {} edges".format(
g_nx.number_of_nodes(), g_nx.number_of_edges()))
Largest connected component: 2485 nodes, 5069 edges
The features of the nodes are taken into account in the model:
feature_names = ["w_{}".format(ii) for ii in range(1433)]
column_names = feature_names + ["subject"]
node_data = pd.read_csv(os.path.join(data_dir, "cora.content"),
sep="\t",
header=None,
names=column_names)
node_data.drop(['subject'], axis=1, inplace=True)
node_data.index = node_data.index.map(str)
node_data = node_data[node_data.index.isin(list(g_nx.nodes()))]
node_data.head(2)
| w_0 | w_1 | w_2 | w_3 | w_4 | w_5 | w_6 | w_7 | w_8 | w_9 | … | w_1423 | w_1424 | w_1425 | w_1426 | w_1427 | w_1428 | w_1429 | w_1430 | w_1431 | w_1432 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 31336 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1061127 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
2 rows × 1433 columns
Define a set of node features that will be used by the model as the difference between the set of all node features and a list of user-defined node attributes to ignore:
feature_names = sorted(set(node_data.columns))
We need to convert node features that will be used by the model to numeric values that are required for GraphSAGE input. Note that all node features in the Cora dataset, except the categorical “subject” feature, are already numeric, and don’t require the conversion.
node_features = node_data[feature_names].values
node_features.shape
(2485, 1433)
Add node data to g_nx:
for nid, f in zip(node_data.index, node_features):
g_nx.node[nid]['label'] = "paper"
g_nx.node[nid]["feature"] = f
Splitting a graph
Splitting graph-like data into train and test sets is not as straightforward as in classic (tabular) machine learning. If you take a subset of nodes you also need to ensure that the edges do not have endpoints across the other set. That is, edges should connect only to train or test nodes but not having endpoints in each set. So, this is in general a little tricky but the StellarGraph framework makes it easy by giving us a method to do this in one line of code. Actually the splitting happens in a slightly different fashion. Instead of taking a subset of nodes all the nodes are kept in both training and test but the edges are randomly sampled. Each of these graphs will have the same number of nodes as the input graph, but the number of links will differ (be reduced) as some of the links will be removed during each split and used as the positive samples for training/testing the link prediction classifier.
From the original graph G, extract a randomly sampled subset of test edges (true and false citation links) and the reduced graph G_test with the positive test edges removed. Define an edge splitter on the original graph g_nx:
edge_splitter_test = EdgeSplitter(g_nx)
Randomly sample a fraction p=0.1 of all positive links, and same number of negative links, from G, and obtain the reduced graph G_test with the sampled links removed:
G_test, edge_ids_test, edge_labels_test = edge_splitter_test.train_test_split(
p=0.1, method="global", keep_connected=True
)
** Sampled 506 positive and 506 negative edges. **
The reduced graph G_test, together with the test ground truth set of links (edge_ids_test, edge_labels_test), will be used for testing the model.
Now repeat this procedure to obtain the training data for the model. From the reduced graph G_test, extract a randomly sampled subset of train edges (true and false citation links) and the reduced graph G_train with the positive train edges removed:
edge_splitter_train = EdgeSplitter(G_test)
G_train, edge_ids_train, edge_labels_train = edge_splitter_train.train_test_split(
p=0.1, method="global", keep_connected=True
)
** Sampled 456 positive and 456 negative edges. **
Defining the GraphSage model
Convert G_train and G_test to StellarGraph objects (undirected, as required by GraphSAGE) for ML:
G_train = sg.StellarGraph(G_train, node_features="feature")
G_test = sg.StellarGraph(G_test, node_features="feature")
Summary of G_train and G_test – note that they have the same set of nodes, only differing in their edge sets:
print(G_train.info())
StellarGraph: Undirected multigraph
Nodes: 2485, Edges: 4107
Node types:
paper: [2485]
Attributes: {'feature', 'subject'}
Edge types: paper-default->paper
Edge types:
paper-default->paper: [4107]
print(G_test.info())
StellarGraph: Undirected multigraph
Nodes: 2485, Edges: 4563
Node types:
paper: [2485]
Attributes: {'feature', 'subject'}
Edge types: paper-default->paper
Edge types:
paper-default->paper: [4563]
Next, we create the link mappers for sampling and streaming training and testing data to the model. The link mappers essentially “map” pairs of nodes (paper1, paper2) to the input of GraphSAGE: they take minibatches of node pairs, sample 2-hop subgraphs with (paper1, paper2) head nodes extracted from those pairs, and feed them, together with the corresponding binary labels indicating whether those pairs represent true or false citation links, to the input layer of the GraphSAGE model, for SGD updates of the model parameters.
Specify the minibatch size (number of node pairs per minibatch) and the number of epochs for training the model:
batch_size = 20
epochs = 20
Specify the sizes of 1- and 2-hop neighbour samples for GraphSAGE:
Note that the length of num_samples list defines the number of layers/iterations in the GraphSAGE model. In this example, we are defining a 2-layer GraphSAGE model.
num_samples = [20, 10]
train_gen = GraphSAGELinkGenerator(G_train, batch_size, num_samples).flow(edge_ids_train,edge_labels_train)
test_gen = GraphSAGELinkGenerator(G_test, batch_size, num_samples).flow(edge_ids_test, edge_labels_test)
Build the model: a 2-layer GraphSAGE model acting as node representation learner, with a link classification layer on concatenated (paper1, paper2) node embeddings.
GraphSAGE part of the model, with hidden layer sizes of 50 for both GraphSAGE layers, a bias term, and no dropout. (Dropout can be switched on by specifying a positive dropout rate, 0 < dropout < 1)
Note that the length of layer_sizes list must be equal to the length of num_samples, as len(num_samples) defines the number of hops (layers) in the GraphSAGE model.
layer_sizes = [20, 20]
assert len(layer_sizes) == len(num_samples)
graphsage = GraphSAGE(
layer_sizes=layer_sizes, generator=train_gen, bias=True, dropout=0.3
)
x_inp, x_out = graphsage.build()
Final link classification layer that takes a pair of node embeddings produced by graphsage, applies a binary operator to them to produce the corresponding link embedding (‘ip’ for inner product; other options for the binary operator can be seen by running a cell with ?link_classification in it), and passes it through a dense layer:
prediction = link_classification(
output_dim=1, output_act="relu", edge_embedding_method='ip'
)(x_out)
link_classification: using 'ip' method to combine node embeddings into edge embeddings
Stack the GraphSAGE and prediction layers into a Keras model, and specify the loss
model = keras.Model(inputs=x_inp, outputs=prediction)
model.compile(
optimizer=keras.optimizers.Adam(lr=1e-3),
loss=keras.losses.binary_crossentropy,
metrics=["acc"],
)
Evaluate the initial (untrained) model on the train and test set:
init_train_metrics = model.evaluate_generator(train_gen)
init_test_metrics = model.evaluate_generator(test_gen)
print("\nTrain Set Metrics of the initial (untrained) model:")
for name, val in zip(model.metrics_names, init_train_metrics):
print("\t{}: {:0.4f}".format(name, val))
print("\nTest Set Metrics of the initial (untrained) model:")
for name, val in zip(model.metrics_names, init_test_metrics):
print("\t{}: {:0.4f}".format(name, val))
Train Set Metrics of the initial (untrained) model:
loss: 0.6847
acc: 0.6316
Test Set Metrics of the initial (untrained) model:
loss: 0.6795
acc: 0.6364
Let’s go for it:
history = model.fit_generator(
train_gen,
epochs=epochs,
validation_data=test_gen,
verbose=2
)
Epoch 1/20
51/51 [==============================] - 2s 47ms/step - loss: 0.6117 - acc: 0.6324
- 7s - loss: 0.7215 - acc: 0.6064 - val_loss: 0.6117 - val_acc: 0.6324
Epoch 2/20
51/51 [==============================] - 3s 53ms/step - loss: 0.5301 - acc: 0.7263
- 7s - loss: 0.5407 - acc: 0.7171 - val_loss: 0.5301 - val_acc: 0.7263
Epoch 3/20
...
Epoch 18/20
51/51 [==============================] - 3s 53ms/step - loss: 0.6060 - acc: 0.8083
- 7s - loss: 0.1306 - acc: 0.9912 - val_loss: 0.6060 - val_acc: 0.8083
Epoch 19/20
51/51 [==============================] - 3s 53ms/step - loss: 0.5586 - acc: 0.7955
- 7s - loss: 0.1258 - acc: 0.9857 - val_loss: 0.5586 - val_acc: 0.7955
Epoch 20/20
51/51 [==============================] - 3s 51ms/step - loss: 0.6495 - acc: 0.7964
- 7s - loss: 0.1193 - acc: 0.9923 - val_loss: 0.6495 - val_acc: 0.7964
You can use tensorboard to see pretty dataviz or you can use a normal Python plot:
import matplotlib.pyplot as plt
%matplotlib inline
def plot_history(history):
metrics = sorted(history.history.keys())
metrics = metrics[:len(metrics)//2]
f,axs = plt.subplots(1, len(metrics), figsize=(12,4))
for m,ax in zip(metrics,axs):
# summarize history for metric m
ax.plot(history.history[m])
ax.plot(history.history['val_' + m])
ax.set_title(m)
ax.set_ylabel(m)
ax.set_xlabel('epoch')
ax.legend(['train', 'test'], loc='upper right')
plot_history(history)
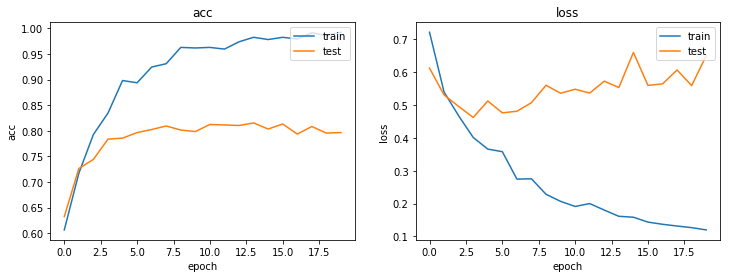
So, how well does our model perform?
train_metrics = model.evaluate_generator(train_gen)
test_metrics = model.evaluate_generator(test_gen)
print("\nTrain Set Metrics of the trained model:")
for name, val in zip(model.metrics_names, train_metrics):
print("\t{}: {:0.4f}".format(name, val))
print("\nTest Set Metrics of the trained model:")
for name, val in zip(model.metrics_names, test_metrics):
print("\t{}: {:0.4f}".format(name, val))
Train Set Metrics of the trained model:
loss: 0.0549
acc: 0.9978
Test Set Metrics of the trained model:
loss: 0.6798
acc: 0.7925
There is space for improvements but this article is in the first place a conceptual invitation not a way to accuracy paradise.