Graph attention networks
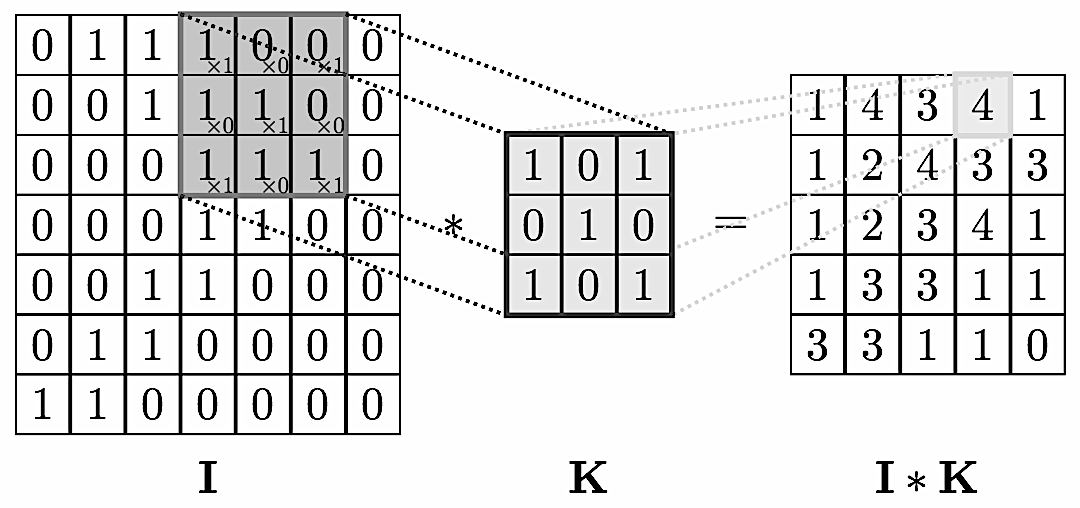
We can think of graphs as encoding a form of irregular spatial structure and graph convolutions attempt to generalize the convolutions applied to regular grid structures. Recall that if you have a grid like below you can glide a convolution matrix over it and the result at each step is the sum of the overlay (not a normal matrix multiplication!). If one looks at the grid as a graph then the convolution is simplified by the fact that one can use a global matrix across the whole graph. In a general graph this is not possible and one gets a location dependent convolution. This immediately infers that it takes more processing to perform a convolution on a graph than on, say, a 2D image.
This location dependence can however also vary in complexity. For example, if you have a central node with data $v_0$ surrounded by neighbors with data $v_i$ you could define a convolution so that the new data $v’_0$ at the node is
$$v’_0 = \sum \frac{1}{d_0\,d_i}v_i$$
with $d_i, d_0$ the vertex degrees. This is a nicely symmetric and easy to compute convolution. A more complex is the attention mechanism where one has an additional layer of complexity and parameters.
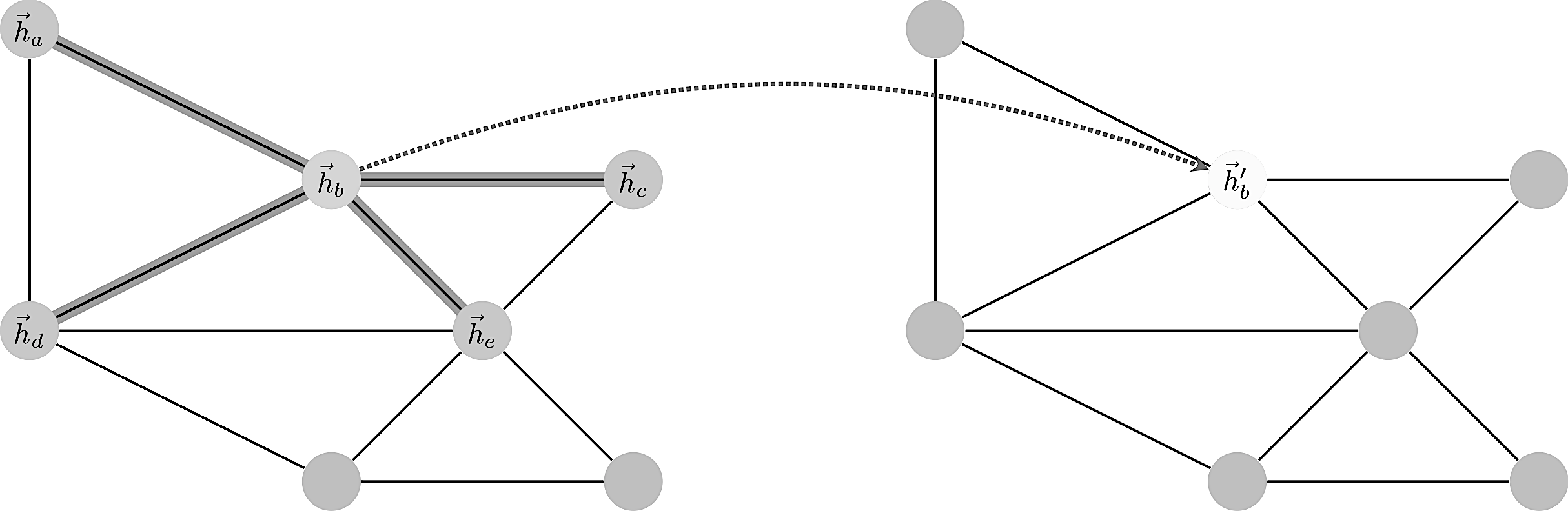
Enumerating the desirable traits of image convolutions, we arrive at the following properties we would ideally like our graph convolutional layer to have:
- Computational and storage efficiency
- Fixed number of parameters (independent of input graph size);
- Localisation (acting on a local neighbourhood of a node);
- Ability to specify arbitrary importances to different neighbours;
- Applicability to inductive problems (arbitrary, unseen graph structures).
Satisfying all of the above at once has proves to be challenging, and indeed, none of the prior techniques have been successful at achieving them simultaneously.
Consider a graph of $n$ nodes, specified as a set of node features $(f_1,\dots,f_n)$ and an adjacency matrix $(A_{ij})$. These two inputs completely define the graph as a structure we wish to work with.
A graph convolution computes a new set $(f’_1,\dots,f’_n)$ via a neural transformation
$$ \sigma ( \sum_{j\in n(i)}\alpha_{ij} f_j )$$
where the sum is over neighbors. The problem with this formula is to make the transformation independent of the local structure. How to define $\alpha$ such that it works in all contexts?
The trick is to let $\alpha_{ij}$ be implicitly defined, employing self-attention over the node features to do so. Self-attention has previously been shown to be self-sufficient for state-of-the-art-level results on machine translation, as demonstrated by the Transformer architecture
We let $\alpha_{ij}$ be computed as a byproduct of an attention mechanism which computes unnormalized coefficients $e_{ij}$ across pairs of nodes based on their features
$$e_{ij}=\alpha(f_i,f_j).$$
$$ f_i \mapsto \sigma(\sum_{j\in n(i)}\alpha(f_i,f_j)\;f_j)$$
Usually a softmax is applied over neighborhood to normalize things:
$$\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{n(i)}\exp(e_{ik})}$$
More details can be found in the original paper or this review paper.
In the following example we use once again the Cora dataset to show how GAT can be used to predict data on the nodes. In this case the ‘subject’ label of the paper represented by the node.
import networkx as nx
import pandas as pd
import os
import stellargraph as sg
from stellargraph.mapper import FullBatchNodeGenerator
from stellargraph.layer import GAT
from keras import layers, optimizers, losses, metrics, Model
from sklearn import preprocessing, feature_extraction, model_selection
Using TensorFlow backend.
See a related article for details about Cora, we simply reproduce a straightforward import to obtain a Stellargraph graph instance.
data_dir = os.path.expanduser("~/data/cora")
edgelist = pd.read_csv(os.path.join(data_dir, "cora.cites"), sep='\t', header=None, names=["target", "source"])
edgelist["label"] = "cites"
Gnx = nx.from_pandas_edgelist(edgelist, edge_attr="label")
nx.set_node_attributes(Gnx, "paper", "label")
feature_names = ["w_{}".format(ii) for ii in range(1433)]
column_names = feature_names + ["subject"]
node_data = pd.read_csv(os.path.join(data_dir, "cora.content"), sep='\t', header=None, names=column_names)
For machine learning we want to take a subset of the nodes for training, and use the rest for validation and testing. We’ll use scikit-learn again to do this.
Here we’re taking 140 node labels for training, 500 for validation, and the rest for testing.
train_data, test_data = model_selection.train_test_split(
node_data, train_size=140, test_size=None, stratify=node_data['subject']
)
val_data, test_data = model_selection.train_test_split(
test_data, train_size=500, test_size=None, stratify=test_data['subject']
)
Note using stratified sampling gives the following counts:
from collections import Counter
Counter(train_data['subject'])
Counter({'Genetic_Algorithms': 22,
'Neural_Networks': 42,
'Theory': 18,
'Reinforcement_Learning': 11,
'Case_Based': 16,
'Probabilistic_Methods': 22,
'Rule_Learning': 9})
The training set has class imbalance that might need to be compensated, e.g., via using a weighted cross-entropy loss in model training, with class weights inversely proportional to class support. However, we will ignore the class imbalance in this example, for simplicity.
For our categorical target, we will use one-hot vectors that will be fed into a soft-max Keras layer during training:
target_encoding = feature_extraction.DictVectorizer(sparse=False)
train_targets = target_encoding.fit_transform(train_data[["subject"]].to_dict('records'))
val_targets = target_encoding.transform(val_data[["subject"]].to_dict('records'))
test_targets = target_encoding.transform(test_data[["subject"]].to_dict('records'))
We now do the same for the node attributes we want to use to predict the subject. These are the feature vectors that the Keras model will use as input. The CORA dataset contains attributes ‘w_x’ that correspond to words found in that publication. If a word occurs more than once in a publication the relevant attribute will be set to one, otherwise it will be zero.
node_features = node_data[feature_names]
train_targets[1:3]
array([[0., 0., 1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0., 0.]])
Now create a StellarGraph object from the NetworkX graph and the node features and targets. It is StellarGraph objects that we use in this library to perform machine learning tasks on.
G = sg.StellarGraph(Gnx, node_features=node_features)
print(G.info())
StellarGraph: Undirected multigraph
Nodes: 2708, Edges: 5278
Node types:
paper: [2708]
Edge types: paper-cites->paper
Edge types:
paper-cites->paper: [5278]
To feed data from the graph to the Keras model we need a generator. Since GAT is a full-batch model, we use the FullBatchNodeGenerator class to feed node features and graph adjacency matrix to the model.
generator = FullBatchNodeGenerator(G, method="gat")
For training we map only the training nodes returned from our splitter and the target values.
train_gen = generator.flow(train_data.index, train_targets)
Now we can specify our machine learning model, we need a few more parameters for this:
- the
layer_sizesis a list of hidden feature sizes of each layer in the model. In this example we use two GAT layers with 8-dimensional hidden node features for the first layer and the 7 class classification output for the second layer. attn_headsis the number of attention heads in all but the last GAT layer in the modelactivationsis a list of activations applied to each layer’s output- Arguments such as
bias,in_dropout,attn_dropoutare internal parameters of the model, execute?GATfor details.gat = GAT( layer_sizes=[8, train_targets.shape[1]], activations=["elu", "softmax"], attn_heads=8, generator=generator, in_dropout=0.5, attn_dropout=0.5, normalize=None )
Expose the input and output tensors of the GAT model for node prediction, via GAT.node_model() method:
x_inp, predictions = gat.node_model()
WARNING:tensorflow:From /Users/swa/conda/lib/python3.7/site-packages/tensorflow/python/ops/control_flow_ops.py:423: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /Users/swa/conda/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:3445: calling dropout (from tensorflow.python.ops.nn_ops) with keep_prob is deprecated and will be removed in a future version.
Instructions for updating:
Please use `rate` instead of `keep_prob`. Rate should be set to `rate = 1 - keep_prob`.
Now let’s create the actual Keras model with the input tensors x_inp and output tensors being the predictions predictions from the final dense layer
model = Model(inputs=x_inp, outputs=predictions)
model.compile(
optimizer=optimizers.Adam(lr=0.005),
loss=losses.categorical_crossentropy,
metrics=["acc"],
)
Train the model, keeping track of its loss and accuracy on the training set, and its generalisation performance on the validation set (we need to create another generator over the validation data for this)
val_gen = generator.flow(val_data.index, val_targets)
Create callbacks for early stopping (if validation accuracy stops improving) and best model checkpoint saving:
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
if not os.path.isdir("logs"):
os.makedirs("logs")
es_callback = EarlyStopping(monitor="val_acc", patience=20) # patience is the number of epochs to wait before early stopping in case of no further improvement
mc_callback = ModelCheckpoint(
"logs/best_model.h5",
monitor="val_acc",
save_best_only=True,
save_weights_only=True,
)
Train the model
history = model.fit_generator(
train_gen,
epochs=50,
validation_data=val_gen,
verbose=2,
shuffle=False, # this should be False, since shuffling data means shuffling the whole graph
callbacks=[es_callback, mc_callback],
)
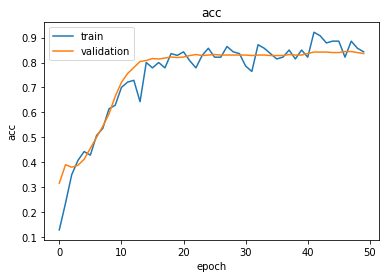
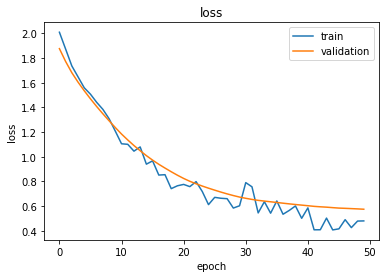
Epoch 1/50
- 2s - loss: 2.0091 - acc: 0.1286 - val_loss: 1.8762 - val_acc: 0.3160
Epoch 2/50
- 0s - loss: 1.8727 - acc: 0.2357 - val_loss: 1.7720 - val_acc: 0.3900
Epoch 3/50
- 0s - loss: 1.7359 - acc: 0.3500 - val_loss: 1.6811 - val_acc: 0.3800
...
Epoch 47/50
- 0s - loss: 0.4901 - acc: 0.8214 - val_loss: 0.5821 - val_acc: 0.8440
Epoch 48/50
- 0s - loss: 0.4258 - acc: 0.8857 - val_loss: 0.5797 - val_acc: 0.8440
Epoch 49/50
- 0s - loss: 0.4788 - acc: 0.8571 - val_loss: 0.5775 - val_acc: 0.8400
Epoch 50/50
- 0s - loss: 0.4801 - acc: 0.8429 - val_loss: 0.5748 - val_acc: 0.8360
Plot the training history:
import matplotlib.pyplot as plt
%matplotlib inline
def remove_prefix(text, prefix):
return text[text.startswith(prefix) and len(prefix):]
def plot_history(history):
metrics = sorted(set([remove_prefix(m, "val_") for m in list(history.history.keys())]))
for m in metrics:
# summarize history for metric m
plt.plot(history.history[m])
plt.plot(history.history['val_' + m])
plt.title(m)
plt.ylabel(m)
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='best')
plt.show()
plot_history(history)
Reload the saved weights of the best model found during the training (according to validation accuracy)
model.load_weights("logs/best_model.h5")
Evaluate the best model on the test set
test_gen = generator.flow(test_data.index, test_targets)
test_metrics = model.evaluate_generator(test_gen)
print("\nTest Set Metrics:")
for name, val in zip(model.metrics_names, test_metrics):
print("\t{}: {:0.4f}".format(name, val))
Test Set Metrics:
loss: 0.6157
acc: 0.8206
Now let’s get the predictions for all nodes:
all_nodes = node_data.index
all_gen = generator.flow(all_nodes)
all_predictions = model.predict_generator(all_gen)
These predictions will be the output of the softmax layer, so to get final categories we’ll use the inverse_transform method of our target attribute specifcation to turn these values back to the original categories
Note that for full-batch methods the batch size is 1 and the predictions have shape $(1, N_{nodes}, N_{classes})$ so we we remove the batch dimension to obtain predictions of shape $(N_{nodes}, N_{classes})$.
node_predictions = target_encoding.inverse_transform(all_predictions.squeeze())
Let’s have a look at a few predictions after training the model:
results = pd.DataFrame(node_predictions, index=all_nodes).idxmax(axis=1)
df = pd.DataFrame({"Predicted": results, "True": node_data['subject']})
df.head(20)
| Predicted | True | |
|---|---|---|
| 31336 | subject=Neural_Networks | Neural_Networks |
| 1061127 | subject=Rule_Learning | Rule_Learning |
| 1106406 | subject=Reinforcement_Learning | Reinforcement_Learning |
| 13195 | subject=Reinforcement_Learning | Reinforcement_Learning |
| 37879 | subject=Probabilistic_Methods | Probabilistic_Methods |
| 1126012 | subject=Probabilistic_Methods | Probabilistic_Methods |
| 1107140 | subject=Reinforcement_Learning | Theory |
| 1102850 | subject=Neural_Networks | Neural_Networks |
| 31349 | subject=Neural_Networks | Neural_Networks |
| 1106418 | subject=Theory | Theory |
| 1123188 | subject=Probabilistic_Methods | Neural_Networks |
| 1128990 | subject=Neural_Networks | Genetic_Algorithms |
| 109323 | subject=Probabilistic_Methods | Probabilistic_Methods |
| 217139 | subject=Neural_Networks | Case_Based |
| 31353 | subject=Neural_Networks | Neural_Networks |
| 32083 | subject=Neural_Networks | Neural_Networks |
| 1126029 | subject=Reinforcement_Learning | Reinforcement_Learning |
| 1118017 | subject=Neural_Networks | Neural_Networks |
| 49482 | subject=Neural_Networks | Neural_Networks |
| 753265 | subject=Neural_Networks | Neural_Networks |
Evaluate node embeddings as activations of the output of the 1st GraphAttention layer in GAT layer stack (the one before the top classification layer predicting paper subjects), and visualise them, coloring nodes by their true subject label. We expect to see nice clusters of papers in the node embedding space, with papers of the same subject belonging to the same cluster.
Let’s create a new model with the same inputs as we used previously x_inp but now the output is the embeddings rather than the predicted class. We find the embedding layer by taking the first graph attention layer in the stack of Keras layers. Additionally note that the weights trained previously are kept in the new model.
emb_layer = next(l for l in model.layers if l.name.startswith("graph_attention"))
print("Embedding layer: {}, output shape {}".format(emb_layer.name, emb_layer.output_shape))
Embedding layer: graph_attention_sparse_1, output shape (1, 2708, 64)
embedding_model = Model(inputs=x_inp, outputs=emb_layer.output)
The embeddings can now be calculated using the predict_generator function. Note that the embeddings returned are 64 dimensional features (8 dimensions for each of the 8 attention heads) for all nodes.
emb = embedding_model.predict_generator(all_gen)
emb.shape
(1, 2708, 64)
Project the embeddings to 2d using either TSNE or PCA transform, and visualise, coloring nodes by their true subject label
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
import pandas as pd
import numpy as np
Note that the embeddings from the GAT model have a batch dimension of 1 so we squeeze this to get a matrix of $N_{nodes} \times N_{emb}$.
Additionally, the GraphAttention layers before the final layer order the embeddings according to the graph order in G.nodes(), so we need to re-index the labels.
X = emb.squeeze()
y = np.argmax(target_encoding.transform(node_data.reindex(G.nodes())[["subject"]].to_dict('records')), axis=1)
if X.shape[1] > 2:
transform = TSNE #PCA
trans = transform(n_components=2)
emb_transformed = pd.DataFrame(trans.fit_transform(X), index=list(G.nodes()))
emb_transformed['label'] = y
else:
emb_transformed = pd.DataFrame(X, index=list(G.nodes()))
emb_transformed = emb_transformed.rename(columns = {'0':0, '1':1})
emb_transformed['label'] = y
alpha = 0.7
fig, ax = plt.subplots(figsize=(7,7))
ax.scatter(emb_transformed[0], emb_transformed[1], c=emb_transformed['label'].astype("category"),
cmap="jet", alpha=alpha)
ax.set(aspect="equal", xlabel="$X_1$", ylabel="$X_2$")
plt.title('{} visualization of GAT embeddings for cora dataset'.format(transform.__name__))
plt.show()